Hi, welcome back to our Hardcaml MIPS project! Before we dive into the actual project, I wanted to provide a bit of background on how hardware and computers work, and why I hope Hardcaml might be a good tool for hardware design. This article is split into 2 parts, see the second one here.
This post assumes a bit of programming experience, but shouldn't require hardware knowledge. That being said, the ramblings of a college student on the internet aren't really a substitute for a Computer Engineering education, so if this subject interests you, I encourage further study/research. Let's get started!
What are computers, really?

At the core, computers are just general-purpose input-output machines. They take some input (e.g. data, user inputs, etc) and a set of instructions (code), and produce output (e.g. files, calculations, graphics, updated GUIs, etc) by running the input through the instructions. Along the way, they read and update a "state" (e.g. reading/writing to the filesystem, database, external APIs, etc),.
The problem is, computers aren't (that we know of) conscious or capable of thought. At the physical level, a computer is a rock that we flattened and threw lighting at. If we want it to do something useful, we'll need to seriously dumb things down.
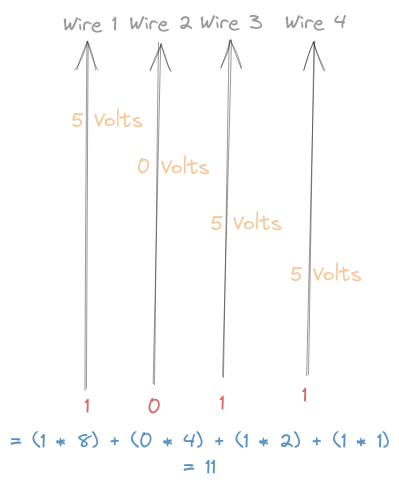
Modern digital computers (i.e. what we usually think of as computers) are made up of wires, which conduct electricity. However, when we use computers, we want to think about values, not electricity. To keep things simple, a single wire can represent 2 values: 1 if it's conducting a lot of electricity, and 0 if it's conducting a little (or no) electricity. This makes it really easy to think about computers and circuits in terms of boolean algebra.
On a quick tangent: if everything's a 0 or a 1, how can we represent larger numbers? Turns out we can just group a bunch of wires together, and have each wire represent a digit in a base-2 number.
The lowest computational level of a computer that's worth thinking about is the logic gate. These are small functions that let us perform boolean algebra on electric signals. For example, the AND gate returns 1 if both its inputs are 1, and 0 otherwise. Some other simple gates are OR and NOT, where the former returns 1 if either input is 1, and the latter inverts a single input (1 => 0, 0 => 1).
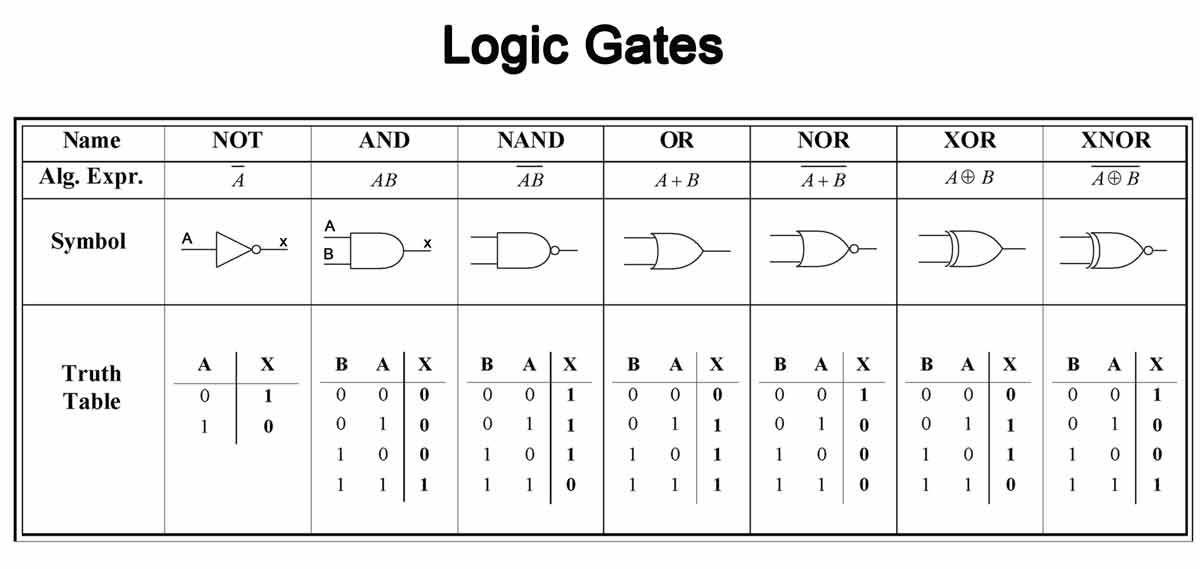
At first glance, these seem too simple to be useful. Luckily for us, we can combine a bunch of them together and make all sorts of cool things, like add (or subtract) 2 numbers, and even multiply and divide. All of the sudden, we can do basic math!
Problem is, it's not enough to calculate: if we want to write non-trivial interesting programs, we need to be able to store various intermediate data. For example, let's say we want to sum a list of N numbers. We can either design circuits for every possible N (an impossible feat), or a single circuit that adds the numbers one at a time to some variable, and finally outputs the variable.
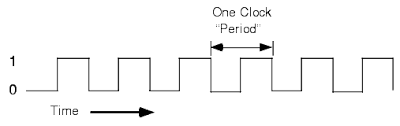
Before we go into storing state/variables, we need to understand how hardware works over time. There's this thing called a clock. Essentially, it's just a wire that alternates between being on (binary 1) and off (binary 0) on a regular interval. The time it takes for the clock to go from 1 to 0 and back to 1 is called a "clock cycle" or "period", and represents a unit of hardware time.
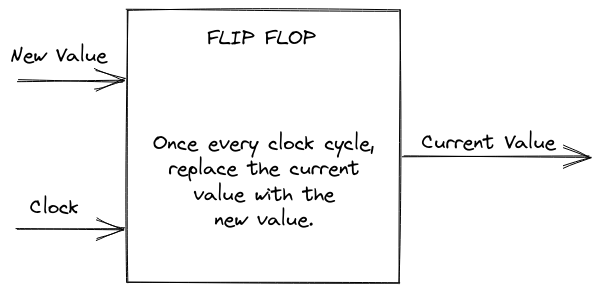
Alright, back to state. Turns out if we make a circuit that uses its own output as one of its inputs, we can use logic gates to make something called a flip-flop (how this works is a bit complicated, I recommend this article. A flip flop stores a single bit, which it constantly emits as an output. It also takes a single bit as input. Once every clock cycle (usually at the moment when the clock changes from 0 to 1), the flip-flop replaces its stored value with the input. If we use multiple flip-flops, we can store an arbitrary variable for a clock cycle. Unsurprisingly, we can wrap a flip flop in a simple logic gate circuit to create a register, which is the hardware equivalent of a variable.
It turns out that we now have everything we need to design hardware: the ability to store and make calculations on arbitrary values. From now on we'll be working at a higher level of abstraction, but before we move on, I want to emphasize 2 types of circuits:
- Combinational circuits are pure functions that produce an output by combining their inputs via some calculation/computation. This includes adding 2 numbers, truncating a value, concatenating 2 values (e.g.
01 <> 10 = 0110), etc.
- Sequential circuits also have a state which they can read/right. For example, if you make a circuit for a counter that increments by
1 every clock cycle, you'll need to store and read its current value.
The MIPS CPU
Let's briefly step away from circuits and revisit computers. When we ask "how do computers work", one of the main things we're interested in is "how do computers do what they do", and as we discussed earlier, computers apply a set of instructions to some input and some current state, producing output and a new state. That's what we'll want to focus on in this project: we want to build a circuit that can process instructions. How do we do this?
First, let's identify what an instruction could be. There's many instruction sets out there, but in this project we'll be using MIPS, a relatively simple instruction set frequently used in university courses (including Penn State's CMPEN331!). Some useful MIPS instructions:
- Arithmetic operations
- Add/subtract/multiply 2 stored values
- Add/subtract/multiply a constant from a stored value
- Bitwise Operations
- Shift a stored value left/right by STORED_VALUE bits
- Take the logical and/or/xor of 2 stored values
- Take the logical and/or/xor of a constant and a stored value
- Memory management
- Load a value from memory, put it in a stored value
- Store a stored value into memory
- Flow Control
- Jump to a different part of the program
- Jump to a different part of the program, but remember where we are now
- Jump to a different part of the program if 2 stored values are equal/not equal
There's more, but those are some of the most important ones.
Before we proceed, I want to clarify my use of "stored value" and "memory". Computers don't remember things like we do, so if they calculate a value and want to use it later, they need to store it somewhere. There are 2 main options:
- Registers (what I referred to previously as "stored values") are storage right on the CPU used for storing intermediate values of calculations. For example, if we're adding a list of numbers, we'd probably put the running sum (also the address of the list in memory and the index of the list element we're currently on) in registers. These are usually implemented as flip-flops and are very fast, but there are very few of them (in MIPS, we can use 32 32-bit registers for instructions to read/write).
- Memory is longer term storage located off the CPU, often as RAM. That's where data used by your program (and the execution stack) is stored. It's a lot cheaper than registers, and there's a lot of it (gigabytes!).
In MIPS, instructions are represented as 32-bit values. This includes an instruction ID (split into "opcode" and "function" segments), information about which registers are used as inputs, and sometimes constant values. For example, 00000001010010110100100000100000 means "add registers 9 and 10, store result in register 11". The first 6 bits represent which instruction it is, and the rest represents which registers should be used for inputs and outputs. Some instructions have slightly different formats: if an instruction represents "jump to address X in the program", we'll store address X instead of input/output registers.
So, how do we process an instruction? One step at a time! The MIPS CPU we'll be designing has 5 stages:
- Fetch. Here, we figure out where we are in the program (stored in a "Program Counter" register) and fetch the next instruction from memory.
- Decode. Here, we figure out what type of instruction we're dealing with, and retrieve the values of any register inputs.
- Execute. Here, we run any calculations needed for the instruction (adds, multiplies, shifts, etc). If applicable, we'll also update our position in the program (via that "Program Counter" register).
- Memory. If our instruction reads/writes to/from data memory, we'll do that here.
- Writeback. If our instruction needs to update a register (for example, to store the result of an
add), we'll do that here.
In addition to making things simpler to understand, this division into stages allows us to compute faster by pipelining several instructions at a time:
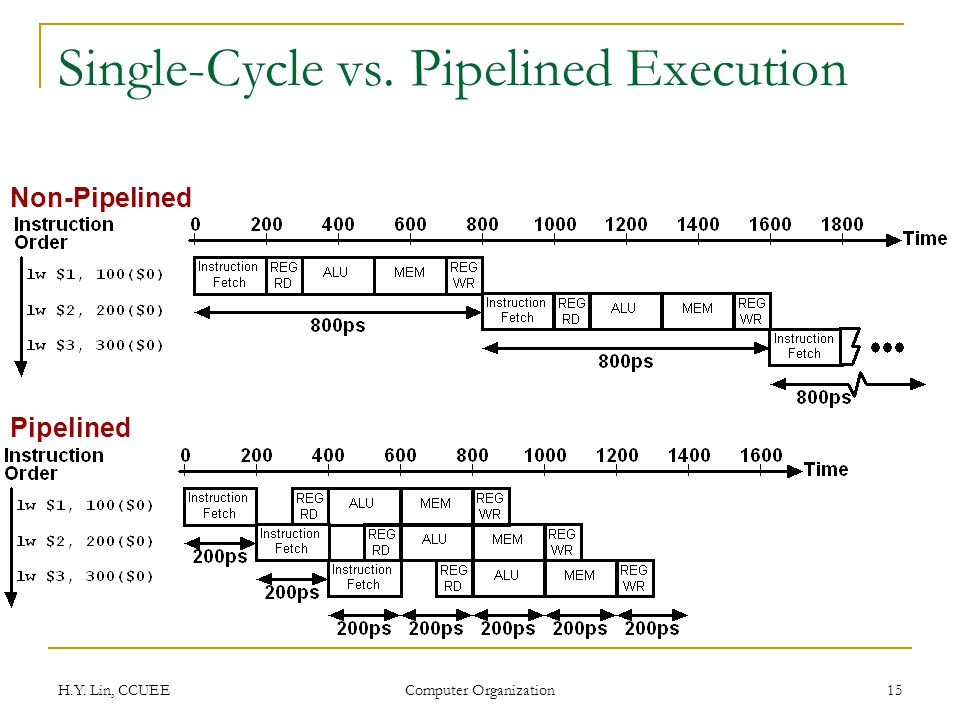
And for now, that's pretty much it! With the instruction set and stages I described above, we can support the vast majority of programs: functions, loops, and ifs included!
In part 2 of this intro, we'll cover how hardware is actually designed, what FPGAs are, and why I hope Hardcaml might be a good fit for designing hardware.