Hi, and welcome back to my OCaml web development project! In the last post, we added a trivial "hello world" Bonsai frontend to our website, and discussed how to build some basic components in Bonsai. In this post, I'll break down several foundational concepts, then explain how Bonsai uses these to provide an elegant, composable, and safe API for building web UIs that perform at scale.
Background Concepts
This section reviews some basic concepts in web development and functional programming that Bonsai is based on.
SPAs and VDOM
Historically, websites would be entirely server-generated. The server side web application would generate HTML in response to each request.
Nowadays, a popular approach to web development is Single Page Applications (SPAs), which partition the frontend and backend of a site. In an SPA, the frontend of a website is a standalone client, much like a mobile app, which is generated dynamically by JavaScript code running in the browser. An SPA frontend communicates with one or more servers to get data (e.g. fetching a list of articles to display) and execute mutations (e.g. creating a comment, signing in/out). This communication can be done over HTTPS, Websockets, RPC, or any other protocol.
Before SPAs became popular, most JavaScript on the frontend would work by directly changing the DOM. For example, if you clicked a button that opened a modal, a JS script would insert the modal's HTML into your page. This made sense for small changes to a static site, but wasn't a great model for dynamic, SPA-generated UIs.
Multiple frameworks, libraries, and approaches for building SPAs were invented over the 2010s. Of particular interest:
- Angular separates components into an HTML template file and a JS/TS component class (as well as optional styles). On the framework level, it updates the DOM for a component when the component's data changes, and updates the data in responds to events in the DOM.
- Svelte compiles SPA source code into compact JS code that surgically updates the DOM without the overhead of a framework runtime.
- React maintains an in-memory, "virtual" representation of the DOM, and updates the real DOM in response to events in the browser to match the virtual DOM.
All have their merits and drawbacks, but Bonsai uses a React-like VDOM model, so that's the one we'll discuss further.

The VDOM model has several advantages:
- The VDOM is very lightweight, so we can compute and frequently update it cheaply. Because a vdom diffing algorithm will keep changes to the actual DOM to the bare minimum, this approach is performant.
- Our unit for representing components is functions that generate vdom from some inputs, and the current state. This lets us apply a functional programming mindset to frontend UI development.
- Components can be nested, making it easy to structure our code as a tree of single-responsibility components.
Components can also include logic to handle events in the DOM (e.g. button clicks / text inputs), as well as lifecycle hooks, which run on component creation / updates / deletion.
Frontend State Management
Component State
Pure components, which output vdom as a function of inputs, are pretty easy to think about. For example, a "user avatar" component would take a user as input, and return something like <img src={user.avatarUrl} />. But things get a bit more challenging when components need to keep track of state.
For state used by a single component, we can take the following approach:
- We define a "Model" for the structure of a component's state. This could be as simple as
Int.t for a counter, or some complex record/variant structure.
- We define a set of "Actions", which represent domain events happening in the component.
- We create a function from the current state and some action to a new state. In other words, how should the state be updated in response to some action?
- Instead of just mapping from inputs to vdom, our "view" function maps from inputs AND the current state to VDOM. We also allow the view function to dispatch actions: for example, we might want to trigger state changes when a button is clicked, if the user hovers over some element, or even when the component is first rendered.
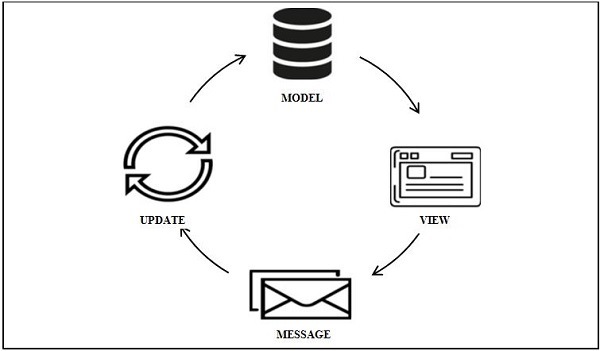
For example, consider the following pseudocode for a counter component:
type model = int;
type action = Increment | Decrement
let apply_action curr_count action =
match action with
| Increment -> curr_count + 1
| Decrement -> curr_count - 1
let view curr_count =
<div>
<button onclick=(fun _ -> dispatch Increment)>+1</button>
<p>{curr_count}</p>
<button onclick=(fun _ -> dispatch Decrement)>-1</button>
</div>
This general idea is similar to React's Redux library, the Elm architecture, and many other frameworks/libraries. It's also what we'll use in Bonsai.
Sharing State
Most complicated UIs will need to share state between components. There's a few patterns we can use, depending on what exactly we want to achieve:
- If state is shared between several components that are close together, we can store state in the "closest common ancestor" component, and pass it down through inputs to child components. See React's Lifting State Up article for examples.
- Sometimes, many components depend on some shared state/environment. For example, let's say we have a UI that can take on one of several themes. We don't want to hardcode a particular theme, so that users can change themes at will. We also don't want to explicitly pass the current theme as an argument to every component, since this would get messy fast. For this case, we want to use something called Context, Dynamic Scope, or Environment, where a root component declares values for some semi-global state, which is then accessible to all the root's subcomponents. For more on this type of state-sharing, read about React's Context.
- In other cases, we might have a bit of state that is read/written to by two components that are very far apart. For example, we could have switches in a sidebar that controls some small part of a separate dashboard. We don't want to lift this state up, since it would need to be passed through many unrelated components. It also doesn't qualify as context, since it's only applicable to a few components. In this case, we'll want to put that state in a global variable, which will only be used by the related components. To be explicit about the behavior of this global variable, we could put it behind a model/action/apply_action pattern like the one described in the last section, except that it would be defined globally instead of in a single component.
Algebraic Effects
In the Component State section above, we described an architecture where things that happen in a component dispatch "actions", which are processed by a handler to update state. We can formally model this through something called "algebraic effects", where the actions are "effects", and the handler is an "effect handler".
So what are algebraic effects? I highly recommend Dan Abramov's Algebraic Effects for the Rest of Us article for a beginner-friendly overview with many examples, but here's the core idea:
In functional programming, we like to structure our code as functions from input to output. Unfortunately for this idealistic viewpoint, we also generally want our code to DO stuff. For example, reading/writing to/from a database, logging something, interacting with the filesystem, getting user input, etc. We could just write this imperative, side-effectful code directly in our functional code, but then we lose the ability to formally describe / reason about the effects a function can use.
In the algebraic effect model, we define "effects", which correspond to "I want to perform some side effect", and separate "effect handlers", which are "how should a given effect be handled". Possible ways to handle an effect include returning a value, performing some asynchronous operation (such as interacting with a database), running an exception handler, etc. This formal definition is much more robust than randomly and arbitrarily interacting with the outside environment. Programs can execute effects at will, and a language-level "effect system" will ensure at compile-time that corresponding handlers for all effects have been defined.
Algebraic effects are't a language-level feature (yet!), but they can be emulated through syntax. We'll see this later with the 'a Effect.ttype and inject functions.
Monads!
Monads are another concept often used in functional programming to deal with side effects. They are notorious for being complicated and hard to understand.

But I'll do my best. You can think of a monad as one of those laboratory gloveboxes that lets scientists work with dangerous materials, without worrying about the side effects (like spontaneously combusting, or accidentally unleashing an alien plague).
Instead of dealing with the value in a monad directly, we give the monad a new function for how to deal with that value, and we get a new monad back with that function applied. Monads come with several operations:
val return: 'a -> 'a t takes some value a and wraps it in some monad.val map: 'a t -> f:('a -> 'b) -> 'b M takes a monad instance containing a value "x" and a function that converts "x" to some other value "y". It then applies the function to the value "x" wrapped in the monad, and returns a new monad containing "y".val bind: 'a M -> f:('a -> 'b M) -> 'b M takes a monad containing a value "x", and a function that converts "x" to some monad containing "y". It then applies the function to the value "x", and outputs the resulting monad.
"Traditional" monads in Haskell only have return and bind, since map can be implemented via bind. However, map can make code a bit cleaner, so most OCaml monads have it.
One common example of a monad is Ocaml's option type:
module Option = struct
type 'a t = Some of 'a | None
let return v = Some v
let bind v f = match v with
| Some v -> f v
| None -> None
let map v f = match v with
| Some v -> Some (f v)
| None -> None
end
The return, bind, and map functions let us specify how we want to change an optional value without worrying if it's defined. For option this isn't strictly necessary, but if the implementation of getting/setting values in a monad was more complicated (e.g. involving external databases), it would offer a very neat interface for manipulating data and executing side effects while keeping implementation separate.
We'll come back to some of these ideas later, but for now, the main things you need to understand are:
- You use monads by defining functions that use the inner value of the monad. You get back the result of that function, wrapped in a monad. You generally don't take the value out of the monad: the alien rock MUST stay in the sciency glove box or humanity ends.
- Monads encapsulate side effects. If you transform an
option monad, and the internal value is None, you'll get an option monad back, not a NullPointerException that crashes your program.
Syntax Shortcuts
One disadvantage of monads is that writing a program as a bunch of function declarations and return/bind calls can result in convoluted, deeply nested code. In OCaml, we can use the ppx_let syntax extension, which allows us to use monad functions with let%bind, let%map, let%sub, and other custom keywords. This is a list of the currently available syntax shortcuts.
This article is a great, example-filled explanation of the syntax's advantages.
On that note, let’s wrap up monads for now, and introduce yet another core concept.
Incremental Computation
Let's say you have a big, complicated webpage, and somewhere on it is a simple counter (like the example discussed above). When the value in the counter changes, we don't want to re-render all the other unrelated parts of the webpage, since they won't have changed. That would be wasteful and inefficient.
Another example of incremental computation is Excel spreadsheets. A complex spreadsheet can have extremely many data cells and formula cells. When one of the data cells changes, we only want to recompute the formulas that depend on that data cell, and the formula cells that depend on those formula cells, and so on. This pattern is also used in build systems such as Make.
Incremental computation breaks a big, complicated computation into many small, composed computations. When an input or state changes, only the affected subcomputations need to be re-run.
An incremental computation can be modeled as a graph, where the nodes are incremental "values" (which can be inputs, some intermediate computations, or the final output), and incoming edges are inputs to a computation. When the value computed at one node changes, only downstream nodes need to be recomputed.
So… Bonsai?
Bonsai is a framework for frontend web development. As you might have guessed from the topics we've covered, Bonsai is:
- Incremental. Generation of VDOM, storage/updating of state, and all other logic that "generates" something in Bonsai is implemented as an incremental computation.
- Backed by monads (kind of). As we saw in the last article, Bonsai components have the
Vdom.Node.t Computation.t type, which is (almost) a monad. Instances of components are Vdom.Node.t Value.t, which is also (almost) a monad.
- Powered by effects. Although it sounds broad, "things that happen", such as DOM events, calls to external servers, and code that runs on component start, are implemented as library-level effects.
Its API consists primarily of the 'a Computation.t and 'a Value.t types, various combinators for operating on them, and primitives for:
- setting/retrieving state used in components and other computations.
- triggering lifecycle events.
We'll cover all this in the remainder of this article.
Computation.t and Value.t
We used Computation.t extensively when going over simple component examples, and I just mentioned there's also a Value.t, but I haven't really explained what these mean. Here goes.
Bonsai's "big idea" is that a Bonsai UI is actually just an incremental computation graph, with a sink (final output) node that produces a Vdom.Node.t. But not every computation needs to produce VDom: the computation pattern generalizes to HTML, state, data, logic, and anything else that goes into building a UI. With this in mind:
- A
'a Value.t is a node in the incremental computation graph. Thinking in Excel, a 'a Value.t is what we see in a cell: it may be a standalone variable, or it might be the output of some formula. It might also change over time, either if we edit the cell (for standalone variables), or if any inputs to the cell's formula change.
- A
'a Computation.t is a blueprint/formula for producing a Value.t. In our Excel analogy, a Computation.t is the formula we see when we double-click a cell.
This distinction is very important. Instances of components, state, or data are Value.ts. Definitions / functions for producing them are Computation.ts. In an analogy to React, a function / class component would be a Computation.t, whereas a <MyComponent /> instance would be a Value.t. This is very important because multiple Value.t instances of a Computation.t DO NOT share state. I'll explain how to apply the state-sharing ideas discussed earlier towards the end of this article.
Also, I hinted earlier that Computation.t and Value.t are kinda monads. What does that mean? Well, they're actually something called an Applicative. You can think of it as a weaker version of a monad without the bind function, only map and return. This makes some things challenging to implement, but is done for good reason.
For an additional explanation of Computation.t and Value.t from Bonsai's authors, see this article.
The let%sub and let%arr Operators
In the last post, we chained let%sub and let%arr keywords to transform the underlying Vdom.Node.t in a Computation.t. These are actually shortcuts for operators called sub and arr.
The sub operator gives us monad-like access to a Value.t instance of a Computation.t, which we must then use to build a new computation.
val sub : 'a Computation.t -> f:('a Value.t -> 'b Computation.t) -> 'b Computation.t
Again, note that each use of let%sub gives a separate Value.t instance which DO NOT share state. So if we were to extend our state example from last time with:
let nested_with_state =
let counter_state = Bonsai.state [%here] (module Int) ~default_model:0 in
let%sub count1, set_count1 = counter_state in
let%sub count2, set_count2 = counter_state in
...
count1 and count2 would not correspond to the same value.
Alright, now we've figured out how to create incremental Value.t nodes from computations. Now, we need to somehow use them to build a new Computation.t, even though we can't directly access the underlying data.
This is where the arr operator comes into play. It allows you to use the data in a Value.t in some function, but wraps the result of that function in a Computation.t.
val arr : 'a Value.t -> f:('a -> 'b) -> 'b Computation.t
The function passed to arr is the actual implementation of a Computation.t, and is what re-runs incrementally. So in the following example:
let component (value1: int Value.t) (value2: int Value.t) (value3: int Value.t) =
let%arr value1 = value1 and value2 = value2 and value3 = value3 in
value1 + value2 + value3
val component : int Value.t -> int Value.t -> int Value.t -> int Computatation.t
We are creating a new computation that takes the incremental nodes value1, value2, and value3 as input, and calculates their sum. Note that unlike with let%sub, where we use a separate keyword for each Computation.t we are instantiating, we have to use a single let%arr, since we want to create a single computation that depends on several incremental values. The benefit of separate let%subs is that we can do the following:
val inner : 'a Computation
val comp_with_input : 'a Value.t -> 'b Computation.t
val parent_comp =
let%sub inner = inner in
let%sub inner2 = (comp_with_input inner) in
...
Which allows us to cleanly use a chain of dependent computations.
So to recap, we can use let%sub to get an instance of an 'a Value.t from an 'a Computation.t blueprint, and let%arr to create a new Computation.t that depends on one or more Value.ts.
Other Component and Value transformations
I'll also note that these aren't the only tools in our arsenal. Both Value.t and Computation.t have map functions, so we can use:
let%map.Computation to create a new Computation.t from other Computation.tslet%map.Value to create a new Value.t from other Value.ts
However, any components that use both Computation.ts and Value.ts will probably need to use the let%sub and let%arr pattern above.
Bonsai also has functions that can further "wrap" some value:
Value.return will turn 'a into 'a Value.tComputation.read will turn 'a Value.t into 'a Computation.tComputation.return will turn 'a into 'a Computation.t
Demonstrative Component Example
Now that we've reviewed some of Bonsai's core ideas, let's consider a heavily annotated example component that showcases state, component composition, and lifecycle hooks:
open! Core
open! Bonsai_web
open Bonsai.Let_syntax
(* This doesn't do anything; it'll be used below to show how we can
* use a component in another component. *)
let header_component = Bonsai.const @@ Vdom.Node.h1 [ Vdom.Node.text "Input" ]
let component =
(* The `Bonsai.state` primitive is a container for a unit of state.
* We immediately use `let%sub` to get it as a `Value.t`.
*)
let%sub value = Bonsai.state [%here] (module String) ~default_model:"" in
(* This could have been done by setting default_model to "something"
* in the `Bonsai.state` primitive.
* Instead, this example demonstrates how lifecycle hooks can be
* used to run effects on computation activation.
*)
let%sub on_activate =
let%arr _, set_value = value in
set_value "something"
in
let%sub () = Bonsai.Edge.lifecycle ~on_activate () in
(* This is the actual rendered component.
* The `sub` combinator gives us a `Value.t` for the header.
* Then we use `arr` to build our final computation from the
* header and state `Value.t` from before.
*)
let%sub header = header_component in
let%arr value, set_value = value and header = header in
Vdom.Node.div
[
header;
Vdom.Node.p [ Vdom.Node.text value ];
Vdom.Node.input
~attr:(Vdom.Attr.on_input (fun _ new_text -> set_value new_text))
[];
]
We'll go over several more interesting examples in future posts. In particular, we'll build a higher-order component that fetches GraphQL queries, and a routing system that showcases how Bonsai can effectively render one of several components.
State with Bonsai
Component State
We discussed a simple component with state in the previous post, but that doesn't really have the full power of the single-component state management paradigm from earlier in this post. Bonsai provides a few primitives for stateful Component.t creation that enable this paradigm:
bonsai.state_machine0 takes separate arguments for the model, action, and action handler. An example implementing counters.bonsai.state_machine1 is similar, but also takes a Value.t as input.bonsai.of_module0 (or 1, or 2) takes a model that includes a model, action, action handler, and 0/1/2 Value.t inputs. An example.bonsai.actor0 (or 1) is like bonsai.state_machine, but also outputs a "response" in addition to the result of the computation. It's used to implement the actor model in Bonsai.
Shared State
Anyways, that's Bonsai's primitives for single-component state. For shared state, all 3 approaches described previously are possible in Bonsai.
"Lifting state up" is the simplest: a parent component can just pass state data/setters (wrapped in Value.t) to inner components as arguments when evaluating them.
"Context" is done through the Bonsai.Dynamic_scope module. You can create an "environment" variable using Dynamic_scope.create, and access its value as a Computation.t with Dynamic_scope.lookup. Then, to evaluate a component tree with some value for a Dynamic_scope variable, you can call Dynamic_scope.set env_var value ~inside:(tree_to_evaluate), which will return a new computation where all uses of Dynamic_scope.lookup env_var will return the set value.
Global variables are a bit tricky. Intuitively, you might think that you could just use Bonsai.state and use it in several components, but recall that each let%sub instantiation of a Computation.t creates a new, unrelated instance. Instead, we can use a Bonsai.Var in the global scope to create a mutable variable that can be shared between components. If you want your components to re-render when the Bonsai.Var.t changes, make sure to access it via Bonsai.Var.value var_instance.
Conclusion
In this post, we did a deep dive into the web development and computer science concepts that underlie Bonsai. We also explored how we can construct an incremental UI with Computation.t, Value.t, and related operators, and how Bonsai components can share and manage state.
I hope this has been useful for gaining a better understanding of Bonsai. It's a challenging framework to learn, and I spent a fair bit of time trying to figure out which operators should be used and when to get the types I needed. But now, I think that Bonsai's approach might be the best I've seen for building safe, massively scalable, performant UIs.
References
In addition to the links throughout this post, here are a few useful references for understanding Bonsai.